Chuyên đề Hệ thức lượng vào tam giác vuông
Với chuyên đề Hệ thức lượng trong tam giác vuông Toán lớp 9 tổng hợp các dạng bài tập, bài tập trắc nghiệm gồm lời giải chi tiết với đầy đủ cách thức giải, lấy một ví dụ minh họa để giúp đỡ học sinh ôn tập, biết cách làm dạng bài tập Hệ thức lượng vào tam giác vuông từ đó đạt điểm cao trong bài bác thi môn Toán lớp 9.
Bạn đang xem: Chuyên đề hệ thức lượng trong tam giác vuông

Một số hệ thức về cạnh và đường cao vào tam giác vuông
A. Phương pháp giải
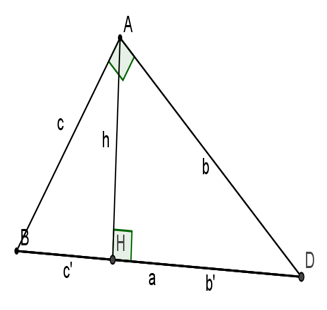
Cho tam giác ABC vuông góc tại A, con đường cao AH. Khi ấy ta có:
1, c2 = ac", b2 = ab"
2, a2 = b2 + c2
3, ah = bc
4, h2 = b".c"
5, 1/h2 = 1/b2 + 1/c2
B. Bài bác tập trường đoản cú luận
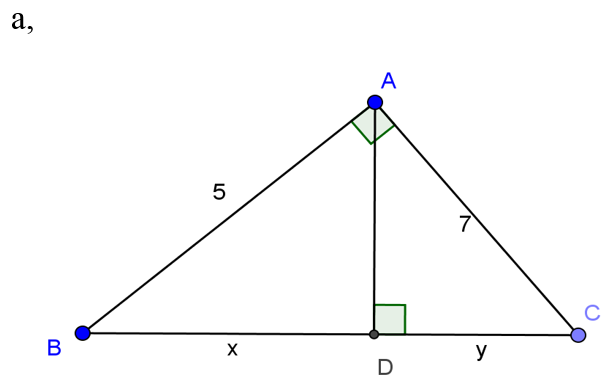
Bài 1: Tính x, y trong những trường hòa hợp sau
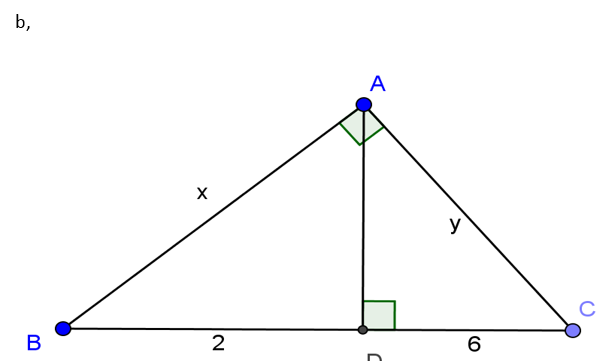
Hướng dẫn giải
a, Áp dụng định lý py-ta-go vào tam giác vuông ABC có:
BC2= AB2+ AC2
BC2= 52+ 72
BC2= 74
Suy ra BC = √74
Áp dụng hệ thức lượng vào tam giac vuông ABC: AB2 = BD.BC
=> BD = AB2/BC => x = 25/√74
DC = BC - BD = √74 - 25/√74 = 49/√74
Vậy x = 25/√74 và y = 49/√74
b) Ta có: BC= BD + DC = 2 + 6 = 8
Áp dụng hệ thức lượng ta có:
AB2= BD.BC = 2.8 = 16. Suy ra AB = 4 xuất xắc x = 4.
AC2= DC.BC = 6.8 = 48. Suy ra AC = √48 xuất xắc y = √48
Bài 2: cho tam giác ABC vuông tại A, con đường cao AH. Tính BC, AC, AH biết AB = 15cm, HC = 16cm.
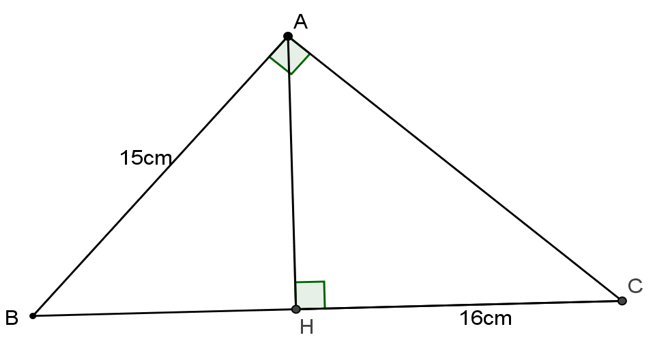
Hướng dẫn giải
Áp dụng hệ thức lượng vào tam giác vuông ABC có:
AC2 = CH.BC = 16.BC
AB2 + AC2 = BC2
⇔ 152 + 16.BC = BC2
⇔ BC2 - 16.BC - 225 = 0
⇔ BC2 - 25BC + 9BC - 225 = 0
⇔ BC(BC - 25) + 9(BC - 25) = 0
⇔ (BC - 25)(BC + 9) = 0
⇔ BC = 25 hoặc BC = -9(loại)
=> AC2 = 16.BC = 16.25 = 400
=> AC = 20
+ Xét tam giác vuông ABC có: AH.BC = AB.AC (hệ thức lượng)
Vậy BC=25(cm); AC=20(cm); AH=12(cm)
Bài 3: mang lại tam giác ABC bao gồm AB = 48cm, BC = 50cm, AC = 14cm. Tính độ dài phân giác giác góc C
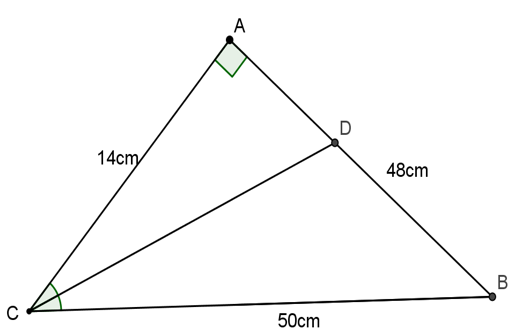
Hướng dẫn giải
Xét tam giác ABC, ta có
BC2 = 502 = 2500
AB2 + AC2 = 142 + 482 = 2500
=> BC2 = AB2 + AC2
=> Tam giác ABC vuông tại A
Có DA/DB = CA/CB = 14/50 = 7/25 (tính hóa học tia phân giác)
=> DB = 25/7 DA.
Ta tất cả DA + DB = AB
⇔ da + 25/7 domain authority = AB ⇔ DA. 32/7 = 48 ⇔ domain authority = 10,5cm
Xét tam giác vuông ACD, theo đinh lí Pi-ta-go ta có
CD2 = AC2 + AD2 = 142 + 10,52 = 306,25 => CD = 17,5cm
Bài 4: cho tam giác ABC vuông trên A, AB=24cm, AC=32cm. Đường trung trực của BC cắt AC, BC theo đồ vật tự D với E. Tính DE.
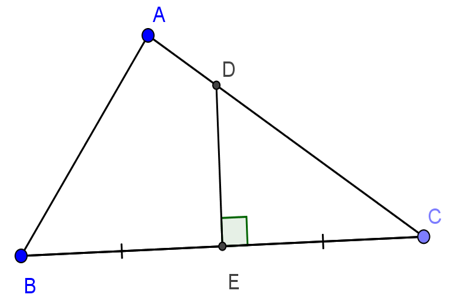
Hướng dẫn giải
Xét tam giác vuông ABC, ta có:
BC2 = AB2+ AC2 ( theo định lý py-ta-go)
BC2 = 242+ 322
BC2 = 1600
BC = 40(cm)
EC = BC : 2 = 40 : 2 = 20(cm)
Xét tam giác vuông ngân hàng á châu acb và tam giác vuông ECD có:
Có ∠A = ∠E = 90o
∠C chung
=> Tam giác ngân hàng á châu ∾ tam giác ECD (g.g)
=> AC/EC = AB/ED
=> ED = AB.EC/AC = 15cm
Vậy ED = 15cm
Bài tập trắc nghiệm Hệ thức lượng vào tam giác vuông
Câu 1: mang lại tam giác ABC vuông trên A bao gồm đường cao AH bắt đầu từ A và AB=3; AC=4. Tính độ nhiều năm đoạn AH
A. 2,5 cmB. 3cmC. 2,4cmD. 2cm
Câu 2: mang đến tam giác ABC vuông trên A, tất cả AB=9cm, AC=12cm. Độ dài con đường cao AH là:
A. 7,2 cmB. 5cmC.6,4 cmD. 5,4cm
Câu 3: mang lại tam giac ABC vuông trên A gồm AB=2cm, AC=4cm. Độ dài đường cao AH là:
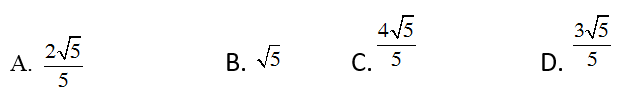
Câu 4: Tam giác ABC vuông trên A, bao gồm AB=2cm, AC=3cm. Lúc ấy độ dài mặt đường cao AH bằng:
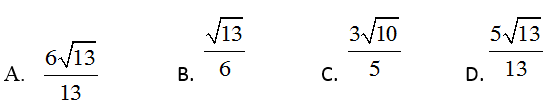
Câu 5: đến tam giác ABC có AH là đường cao bắt nguồn từ A, hệ thức nào dưới đây chứng minh tam giác ABC vuông trên A
A.BC2 = AB2 + AC2
B.AH2 = HB.HC
C.AB2 = BH.BC
D.A, B, C đều đúng.
Câu 6: đến tam giác ABC gồm đường cao xuất phát điểm từ A. Nếu như ∠BAC = 90o thì hệ thức nào dưới đây đúng?
A.BC2 = AB2+AC2
B.AH2 = HB.HC
C.AB2 = BH.BC
D.A, B, C mọi đúng.
Câu 7: đến tam giác ABC tất cả và AH là con đường cao xuất phát điểm từ A. Câu nào sau đấy là đúng?

Câu 8: Tam giác ABC vuông có đường cao AH( H nằm trong cạnh BC). Hình chiếu của H bên trên AB là D, trên AC là E. Câu nào tiếp sau đây sai:

Câu 9: cho tam giác ABC nội tiếp mặt đường tròn đường kính BC=10cm. Cạnh AB=5cm, thì độ dài đường cao AH là:
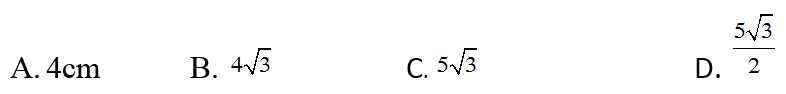
Hướng dẫn giải và đáp án
Câu 1: Áp dụng định lý py-ta-go vào tam giác vuông ABC có:
BC2=AB2+AC2
Thay số ta tính được BC=5.
Áp dụng hệ thức lượng vào tam giác ABC có: AH.BC = AB.AC
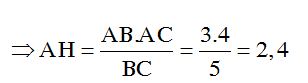
Vậy chọn đáp án:C
Câu 2: lựa chọn đáp án: A
Câu 3: lựa chọn đáp án: C
Câu 4: chọn đáp án: A
Câu 5: chọn đáp án: D
Câu 6: lựa chọn đáp án: D
Câu 7: chọn đáp án: C vày ∠B + ∠C = 90o suy ra tam giác ABC vuông tại A.
Câu 8: lựa chọn đáp án: D vì:
+ Đáp án A đúng do AEHD là hình chữ nhật(vì gồm 3 góc vuông) buộc phải 2 đường chéo AH với DE bằng nhau.
Xem thêm: Flow Là Gì Trong Rap Per Nhất Định Phải Biết, Flow Là Gì Trong Rap
+ Xét tam giác ABC bao gồm :
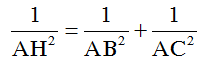
Vì AH = DE cần đáp án B đúng
Từ kia suy ra chọn lời giải D
Câu 9: vị tam giác ABC nội tiếp đường tròn 2 lần bán kính BC = 10cm bắt buộc tam giác ABC vuông tại A. Áp dụng định lý Py-ta-go ta có: AC2 = BC2 - AB2.
Thay số vào ta tính được: AC= √75cm = 5√3 cm.
Áp dụng hệ thức lượng vào t tam giác vuông ABC có: AH.BC = AB.AC.
Thay số vào ta tính được: AH = 5√3/2 centimet
Vậy chọn đáp án: D
Câu 10: đến tam giác ABC vuông tại A, biết AB:AC=3:4, BC=15cm. Độ nhiều năm cạnh AB là:A. 9cmB. 10cmC. 6cmD. 3cm
Câu 11: Hình thang ABCD vuông góc làm việc A, D. Đường chéo BD vuông góc với kề bên BC biết AD=12cm, BC=20cm. Độ dài cạnh AB là:
A.256/13cmB.9cm tốt 16cm
C.16cmD.Một kết quả khác
Câu 12: mang đến tam giác DEF vuông trên D, có DE=3cm, DF=4cm. Lúc đó độ lâu năm cạnh huyền bằng:A.5cmB. 7cmC.6cmD.10cm
Câu 13: cho tam giác ABC vuông trên A, mặt đường cao AH. Biết AB=5cm, BC=13cm. Lúc đó độ nhiều năm đoạn bh bằng:
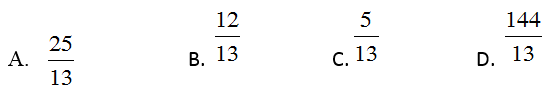
Câu 14: Tam giác ABC vuông trên A, con đường cao AH. Biết AB=3cm, AC=4cm. Khi ấy độ dài đoạn bảo hành bằng:
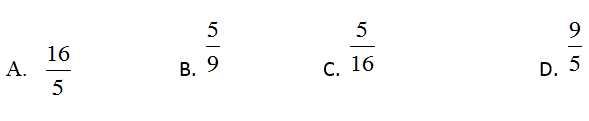
Hướng dẫn giải với đáp án
Câu 10: gọi độ dài cạnh AB = 3x thì độ nhiều năm cạnh AC = 4x. Áp dụng định lý py-ta-go ta được:
⇔ 100 = 9x2 + 162
⇔ x2 = 100 : 25
⇔ x = 2
Từ kia suy ra AB = 6cm
Câu 11: Kẻ BI ⊥ DC. Khi ấy ABID là hình chữ nhật đề xuất AD = BI; AB = DI = 12cm.
Xét tam giác vuông BIC có: IC2=BC2-BI2
Suy ra IC = 16cm.
Xét tam giác vuông BDC .Theo hệ thức lượng ta có: BI2 = DI.IC
Thay số:162 = DI . 13.Tứ kia suy ra DI = 256/13 cm.
Vậy chọn lời giải A
Câu 12: chọn đáp án: A
Câu 13: Áp dụng hệ thức lượng: AB2 = BH.BC
Thay số ta được: 52=BH.13.Suy ra bảo hành = 25/13
Vậy lựa chọn đáp án: A
Câu 14: chọn đáp án: D
Tỉ con số giác của góc nhọn
A. Phương pháp giải
1. Định nghĩa những tỉ số lượng giác của góc nhọn:
1, sin α = AB/AC
2, cos α = BC/AC
3, chảy α = AB/BC
4, cotgα = BC/AB
2. Một số tính chất của những tỉ số lượng giác
+ đến hai góc α với β phụ nhau. Lúc đó:
sin α = cos β
cos α = sin β
tan α = cotg β
cotg α = chảy β
+ mang đến góc nhọn α. Ta có:
0 2B ; CH = a sin2 B
b, Suy ra AB2 = BC.BH ; AH2 = BH.HC
Hướng dẫn giải
a, bệnh minh:
Xét tam giác vuông ABH, ta có:
AH = sinB.AB (1)
Xét tam giác vuông ABC, ta có:
AB = BC.cos B = acos B (2)
Từ (1) với (2) ta có:
AH = a sin B cos B
Tương từ ta có:
+ Xét tam giác vuông ABH: bh = AB.cos B
Xét tam giác vuông ABC: AB = BC.cos B = acos B => bh = a cos2B
+ Xét tam giác vuông ACH: CH = AC.cos C = AC.sin B
Tam giác vuông ABC: AC=BC.sin B=a.sin B => CH = a sin2 B
b, AB2 = a2 cos2B
BC.BH = a.a.cos2B = a2cos2B
=> AB2 = BC.BH
AH2 = a2sin2cos2B
=> AH2 = BH.HC
Bài 2: Giải tam giác trong số trường phù hợp sau( làm cho tròn đến chữ số thập phân sản phẩm nhất).(Tức là tìm toàn bộ các yếu hèn tố chưa biết của tam giác ABC)
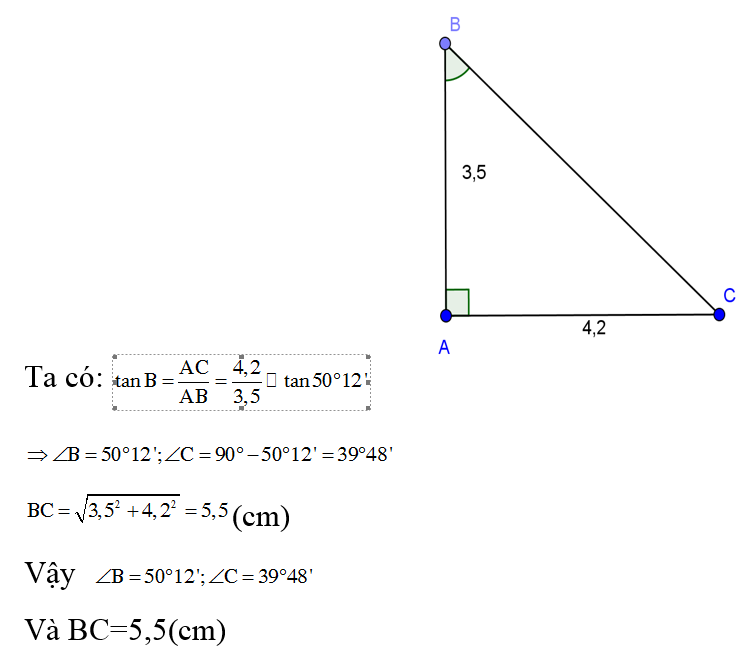
a, Tam giác ABC vuông trên A, biết AB = 3,5; AC = 4,2.
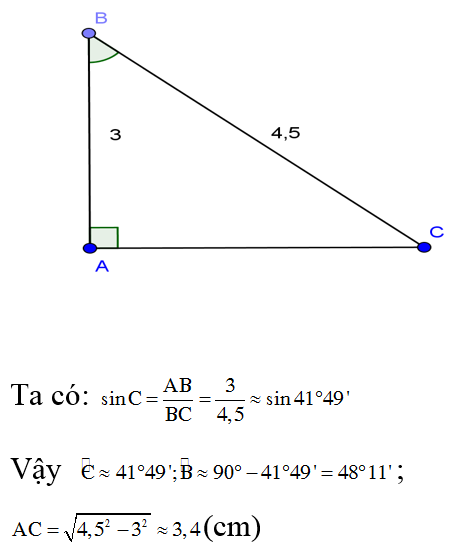
b, Tam giác ABC vuông trên A, biết ∠B = 50o ; AB = 3,7.
Hướng dẫn giải
Bài 3: Giải tam giác ABC, biết ∠B = 65o; ∠C = 40o và BC = 4,2 cm.
Hướng dẫn giải
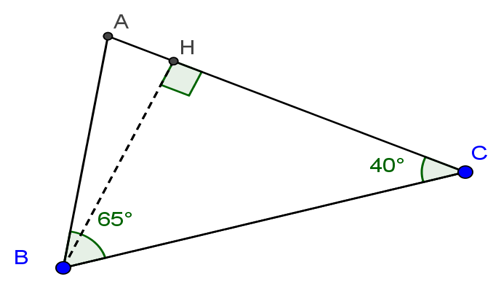
Ta có: ∠A = 180o - (65o + 45o) = 75o
Vẽ bảo hành ⊥ AC
+ Xét tam giác vuông HBC vuông trên H, theo hệ thức về cạnh và góc vào tam giác vuông, ta có:
BH = BC.sin C = 2,7 (cm)
Và CH = BH.cotg C (1)
+ Xét tam giác vuông ABH trên H, theo hệ thức về cạnh cùng góc vào tam giác vuông ta có: